Impermanent Loss is the unrealized loss that occurs when your share of a liquidity provider position becomes uneven compared to its original position.
If you know what all that meant, great! You don’t have to read this article. However, if you were as clueless as we were a few weeks ago, stick around and you’ll be able to explain the concept of impermanent loss to your grandmother.
Let’s dig in.
What is Impermanent Loss?

First off, impermanent loss (IL) only happens to people who provide liquidity to a liquidity pool.
Secondly, impermanent loss is easiest to explain through examples, so we are going to go through two example situations.
Let’s say you put up 100 ETH and $10,000 into a liquidity pool. Most liquidity pools want there to be a 50:50 ratio when you deposit, so we can reasonably assume the price of 1 ETH is $100 in this example. So there is $10,000 worth of a stablecoin and $10,000 worth of ETH.
So you take that total $20,000 and put it into the liquidity pool hoping to gain a profit on some of the fees that happen within the pool. Time for our first example.
Example 1: ETH price rises to $110
Let’s say a trader comes along and realizes he can buy ETH at your liquidity pool and sell it to Coinbase for $110. He keeps buying more and more and the algorithm keeps charging him more until he stops making money.
That’s how these decentralized exchanges work—you pay more and more for each asset you want to buy so it never runs out of that asset to sell you.
However, in our case, the asset was much cheaper than another exchange, so it created an arbitrage opportunity for a trader. If we do the math, we figure out he was able to give $488 and buy 4.652 ETH until the liquidity pool price was also $110.
If he bought any more ETH, he would be losing money. So he immediately sold this cheaper ETH for $511.82 to Coinbase, making a profit of $23.82 by buying and selling to two different liquidity pools.
Now, let’s take the stance of the liquidity provider. This means there is now $10,488 in the pool and 95.347 ETH in the pool (at least in terms of his share).
If we take 95.347 and multiply it by $110—because that’s the going price of ETH—we get 10,488. So 10,488 + 10,488 gives us a total value of $20976.
So the liquidity provider now has a total value of $20976, making a nice $976 because ETH went up. He made some decent money today!
However, to calculate impermanent loss, we need to calculate how much money he WOULD’VE had if he didn’t give money to the liquidity pool and just held it instead.
So he would’ve still had his initial $10,000, but what about if he held his 100 ETH? That 100 ETH is now worth $11,000, so he would’ve had a total of $21,000.
This means he has a total impermanent loss of $21,000 – $20,976, which is $24. In short, this liquidity provider would’ve made more money if he had just held onto his ETH and stablecoin.
This might not seem like much, but imagine a similar scenario where the price jumps 20% instead of 10%, or where the price dropped by half.
In short, impermanent loss is caused when the price difference between two assets in a pool change. As the change increases, so does the impermanent loss.
If ETH goes back to $100, then the impermanent loss is basically cancelled and there is none, because both assets would be the same as when the liquidity provider initially invested.
They call it impermanent loss because it only becomes permanent whenever you cash out your liquidity. Until you do that, there is still an opportunity for the loss to normalize itself out.
Impermanent loss is the loss you get when you have less money compared to the value of our assets that you had if you would’ve just held them, compared to investing them in a liquidity pool.
Example 2: ETH price lowers to $60
Let’s consider another example. This time we start off with 100 ETH and $10,000 in a liquidity pool, however ETH price drops from $100 to $60 on Binance.
So a trader comes along, buys ETH at Binance and sells it to the liquidity pool, starting at $100 and then keeps selling at a lower and lower price until the liquidity pool can’t offer anything higher than $60 for each ETH.
Using the math of a Constant Product Automated Market Maker, we find out this means the trader gave the pool 30 ETH. So they bought 30 ETH for $60 each at Binance, costing them $1800.
Let’s see how much they made.
1,000,000 divided by 130 ETH gives us $14,285, which means the pool should have $7692, however it has $10,000. This means the trader received the difference for giving the pool 30 ETH. This is the math behind the algorithm, so if you don’t get it, don’t pay too much attention to it.
In short, the trader bought ETH at $1800 and sold for $2307, earning $507.
Let’s take a look at our liquidity provider now.
They have 130 ETH at a market price of $60. This means the value of ETH in their portion of the pool is $7800. The cash value in the pool is $7692. This means the value of the assets in the liquidity pool equals $15,292. A sharp loss from the initially invested $20,000.
Now, let’s calculate their impermanent loss. If they didn’t invest their assets, they would’ve had $10,000 cash and 100 ETH, which would be worth $6000, which means their initial investment would only $16,000. $16,000 – $15,292 = an impermanent loss of $708.
We hope you’re understanding how this works.
How It Works
Essentially what you need to know is that it’s good for any liquidity provider when two assets stay roughly the same price.
When one goes up and the other stays the same, the liquidity provider starts to experience impermanent loss and can only recover if the first asset starts to come down to equal out the liquidity.
It gets really tricky when both assets’ prices start moving. In short, if they go in opposite directions, the liquidity provider starts to lose money really fast. However, if they increase the same or decrease the same, the liquidity provider may not lose money due to impermanent loss at all, and may reap the rewards of profits from the trading fees.
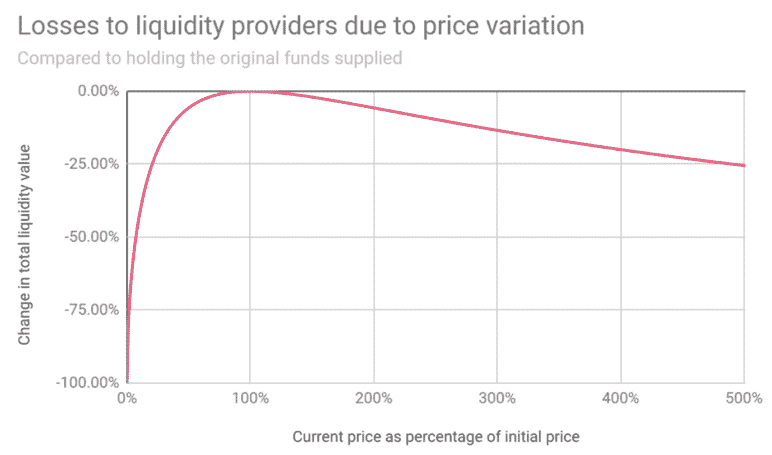
Here is a neat little chart you can look at to see how much impermanent loss a liquidity provider may experience in terms of how much that asset changes in price.
As the price of an asset increases past 100% of it’s value to the other asset, the impermanent loss grows, and as the price of an asset decreases less than 100%, the impermanent loss grows.
Conclusion
As we end this article, we want to let you know we have another article that explains how to reduce or mitigate your risk as a liquidity provider.
We hope you enjoy this article, but most of all we hope you learned something. Thanks for reading, and we’ll see you in the next one!

